Задача 63: Лесной пожар (XIII Всероссийская олимпиада по
информатике)
В МЧС поступило сообщение о возможном
лесном пожаре в заданном квадрате тайги. Для поиска места возгорания
было послано N самолетов. Однако ни один из экипажей пожара не
обнаружил.
Известно, что с самолета видна полоса тайги, границы которой
находятся на расстоянии 50 км справа и слева от той линии на
поверхности Земли, над которой пролетает самолет (см. рисунок),
причем точки, находящиеся на расстоянии ровно 50 км от этой линии,
все еще видны. Донесение с каждого самолета содержало информацию о
том, в каких двух различных точках (xb , yb ) и (xe , ye ) самолет
входил в заданный квадрат и покидал его соответственно. Между этими
точками самолет двигался строго по прямой.
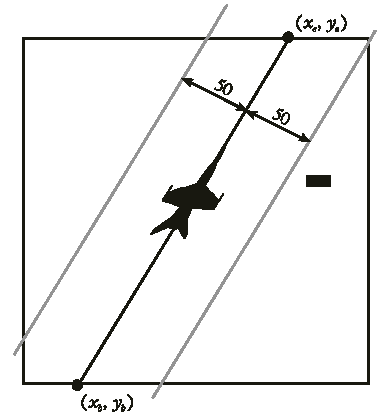
Рис. 5
Требуется
Написать программу, которая определит, действительно ли весь
заданный квадрат тайги был просмотрен с самолетов. Если это не так,
то программа должна находить координаты какой-нибудь точки, лежащей
внутри или на границе квадрата и не попавшей ни в одну из
просмотренных полос.
Входные данные
Входной файл с именем FIRE.IN состоит из N + 2 строк.
В первой строке записано натуральное число L - размер заданного
квадрата тайги в километрах (0 < L <= 1000). Во второй строке -
натуральное число N (1 <= N <= 100) - количество самолетов. В каждой
из последующих N строк записано донесение с самолета - четыре
вещественных координаты xb , yb , xe , ye . Координаты заданы в
километрах. Стороны квадрата тайги параллельны осям координат, его
левый нижний угол находится в точке с координатами (0, 0), а правый
верхний - в точке (L, L).
Выходные данные
Выходной файл с именем FIRE.OUT должен содержать одну строку. Если
заданный квадрат был просмотрен полностью, то эта строка должна
состоять из слова OK, написанного заглавными латинскими буквами. В
противном случае в этой строке должны быть записаны через пробел
координаты x и y какой-либо точки, которая не попала ни в одну из
просмотренных полос. Координаты нужно выводить в километрах с
ошибкой не более одного метра.
Пример входного файла
245
1
26.1 0 193.568 245
Пример выходного файла для приведенного примера входного
файла
155.123 100
Примечание. Будут отдельно оцениваться решения, сделанные в
предположении, что каждый самолет летел параллельно одной из сторон
квадрата.
 Решение: предоставлено Е.В.
Андреевой
Решение: предоставлено Е.В.
Андреевой
Несмотря на то, что ширина каждой из полос составляет 100 км,
непросмотренный участок может быть как угодно малым, то есть его
размер по каждой из координат может быть менее одного метра. Поэтому
искомый результат следует трактовать так: в окрестности найденной
при решении точки должна действительно находиться по крайней мере
одна непросмотренная точка, и каждая из координат этой
непросмотренной точки должна отличаться не более чем на один метр от
координат найденной точки. Поиск такой точки можно осуществлять
следующим образом. Рассмотрим набор отрезков, который состоит из
четырех сторон квадрата и 2N отрезков, образованных в результате
пересечения границ полос с квадратом. Найдем все попарные
пересечения этих 2N + 4 отрезков. Если непросмотренная точка
существует, то она находится в окрестности одной из найденных точек
пересечения.
Рассмотрим 4 угла, образованные в результате пересечения двух
отрезков, обозначив точку их пересечения A (если хотя бы один из
отрезков является стороной квадрата, то рассматривать следует лишь
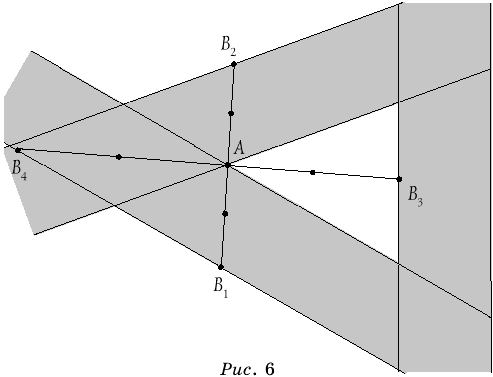
углы, лежащие внутри квадрата). Для каждого из углов найдем точки
пересечения их биссектрис с ближайшим отрезком, не проходящим через
точку A, обозначим их B1 , B2 , B3 , B4 (см. рис. 6). Тогда, для
того чтобы проверить, не является ли один из рассматриваемых углов в
некоторой окрестности точки A непросмотренным с самолетов,
достаточно проверить принадлежность полосам середин отрезков [A; Bi
], i = 1..4. Причем, если в точке A пересекаются более чем 2
отрезка, то опять же достаточно рассматривать лишь попарные их
пересечения, так как если непокрытый угол в окрестности точки A
существует, то он образован в результате пересечения какой-либо пары
отрезков и предложенный выше способ анализа углов позволит
обнаружить точку, непокрытую полосами. Если же непросмотренных
областей нет в окрестности ни одной из точек пересечения отрезков,
то их нет вообще.
Задачу можно решать
и численно. Проверим, не покрыты ли все 4 вершины квадрата одной из
полос или не является ли одна из вершин квадрата непросмотренной ни
из одного самолета. В любом из этих двух случаев задача решена
(квадрат просмотрен полностью с одного самолета в первом случае и
непросмотренная точка найдена - во втором). В противном случае делим
исходный квадрат на 4 части (разделив пополам каждую из сторон) и
анализируем вершины каждого из этих четырех квадратов, и т.д. Причем
квадраты, все четыре вершины которых покрыты одной и той же полосой,
из дальнейшего рассмотрения исключаются. В результате либо будет
найдена непокрытая точка, либо размер квадрата достигнет величины,
которой можно пренебречь в сравнении с машинной точностью
вычислений, и тогда его можно считать просмотренным. Данный метод
будет особенно эффективным, если исключить из рассмотрения касания
полос, то есть считать две и более касающихся полосы за одну и ту же
полосу (что по условию задачи является верным).
Далее
ð


