Задача 62: Телеметрия (XIII Всероссийская олимпиада по информатике)
Для космического корабля
сконструирована телеметрическая система, содержащая N (1 <= N <=
1000) групп датчиков. Каждая из этих групп включает Pi (1 < Pi )
датчиков. Группе датчиков соответствует свой канал связи, к которому
в конкретный момент времени может быть подключен только один датчик
этой группы, который назовем активным.
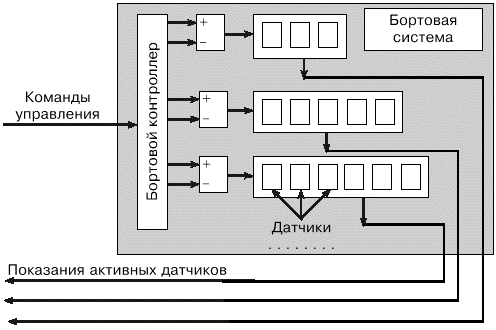
Рис.3
С центрального
пульта на систему могут подаваться команды управления. Каждая
команда управления имеет вид:
номер группы <пробел> + | -
При этом номер активного датчика в соответствующей группе увеличится
или уменьшится на единицу. Попытка установить номер активного
датчика в группе вне пределов [1..Pi ] ведет к аварийному останову
контроллера.
В исходном состоянии для каждой из групп известен номер активного
датчика.
Для комплексной проверки корабля требуется проводить съем показаний
для всех возможных комбинаций активных датчиков, причем повторять
уже использованные ранее комбинации активных датчиков запрещается.
Общее количество комбинаций активных датчиков не превосходит 10 000.
После окончания проверки система должна оказаться в исходном
состоянии.
Требуется
Разработать программу, которая осуществляла бы управление
контроллером, реализующее требуемый опрос датчиков.
Входные данные
Входной файл с именем TELE.IN содержит следующие три строки. Первая
строка содержит число N - количество групп датчиков. Вторая строка
содержит N чисел P1 , P2 , :, PN , каждое из которых задает
количество датчиков в соответствующей группе. Третья строка содержит
N исходных номеров активных датчиков в группах. Числа во второй и
третьей строках разделены пробелом.
Выходные данные
Выходной файл с именем TELE.OUT должен содержать следующие строки. В
первую строку выводится сообщение Yes или No, в зависимости от того,
возможно или нет реализовать управление контроллером, осуществляющее
требуемую схему съема данных. При выводе сообщения Yes в последующих
строках выдается последовательность команд управления. Каждая строка
должна содержать по одной команде управления. При этом знак "+"
соответствует увеличению на 1, а знак "-" - уменьшению на 1 номера
активного датчика в этой группе.
Пример входного файла
2
2 3
2 1
Пример выходного файла, соответствующего приведенному
входному файлу
Yes
1 -
2 +
2 +
1 +
2 -
2 -
Примечание. Будут отдельно оцениваться решения для частных
случаев N = 1, N = 2, N = 3.
 Решение: предоставлено
Е.В. Андреевой
Решение: предоставлено
Е.В. Андреевой
Эта задача являлась, пожалуй, самой сложной на данной олимпиаде, как
по выработке алгоритма решения, так и по его реализации, именно
поэтому даже разбор случаев с N <= 3 оценивался жюри достаточно
высоко. Решать задачу удобнее всего с помощью рекурсивного спуска,
выражая решение для N групп датчиков через перечисление всех
состояний для N - 1 групп датчиков и т.д. Для двух групп решение
строится явным образом. Заметим, что при N = 1 решения не
существует, если данная группа состоит более чем из одного датчика.
При N > 1 решения не существует, если количество датчиков во всех
группах нечетно, то есть произведение чисел P1 , P2 , :, PN нечетно.
Так как если нам требуется перебрать все комбинации активных
датчиков, то в каждой из групп датчиков количество команд "увеличить
номер активного датчика" должно совпадать с количеством команд
"уменьшить номер активного датчика", то есть общее количество
команд, равное числу всевозможных комбинаций, должно быть четным.
Если же существует хотя бы одна группа с номером i, в которой
количество датчиков Pi четно, то решение построить можно. Для
удобства далее будем считать, что i = N, а в начальный момент
времени активным является первый датчик в каждой из групп, что не
снижает общности рассмотрения. Для N = 2 задачу можно
переформулировать следующим образом. В прямоугольнике размером P1 <=
P2 требуется циклически обойти все точки с целочисленными
координатами, построив для этого замкнутую ломаную без
самопересечений и самокасаний. Так как по нашему предположению P2
четно, то решение всегда можно построить следующим образом:

Рис. 4
Если N = 3, то
требуется обойти уже все целочисленные точки прямоугольного
параллелепипеда P 1 <= P2 <= P3 . Для этого сначала обойдем все
точки (x, y, z) параллелепипеда, за исключением тех, у которых x =
1, в таком порядке: значение z фиксируется, и точки, у которых 1 < x
<= P1 , 1 <= y <= P2 , z = 1, обходятся "змейкой", аналогичной
приведенной для N = 2, но без возврата в начальную точку. Затем
делаем z = 2 и обходим точки "второго уровня" такой же "змейкой", но
в обратном направлении, завершая обход в точке (2, 1, 2), затем
переходим в точку (2, 1, 3) и проходим уже "третий уровень"
аналогично первому. Так как P3 четно, то остановимся мы в точке (2,
1, P3 ). Оттуда перемещаемся в соседнюю точку (1, 1, P3 ) и
"змейкой" же обходим оставшуюся грань z = 1, постепенно спускаясь
вниз, и, опять же благодаря четности P3 , оказываемся в начальной
точке (1, 1, 1). Для N > 3 будем поступать подобным же образом.
Сначала обойдем все точки N-мерного параллелепипеда, за исключением
тех, у которых координата x равна 1, заканчивая обход в точке (2, 1,
1, :, PN ), а затем возвращаемся в начальную точку, обходя все точки
с x = 1.
Далее
ð


