Задача 57: Метро (Белорусская олимпиада по информатике 2002)
В некотором городе есть метро,
состоящее из N (1 <= N <= 1000) станций и M линий, соединяющих их.
Каждая линия обеспечивает проезд между какими-то двумя станциями в
обе стороны. Между любой парой станций проведено не более одной
линии. Сеть метро построена таким образом, чтобы с каждой станции
можно было проехать на каждую (возможно, через промежуточные
станции). Назовем это свойство связностью метро.
В связи с изобретением принципиально нового вида транспорта метро
стало убыточным, и его работу решили прекратить. На заседании мэрии
города было постановлено закрывать каждый год по одной станции, но
так, чтобы связность метро каждый раз сохранялась. При закрытии
какой-либо станции, линии, ведущие из этой станции в другие,
естественно, тоже перестают функционировать.
Задание. По введенной информации о сети метро разработать
какой-либо порядок закрытия станций, при котором метро всегда будет
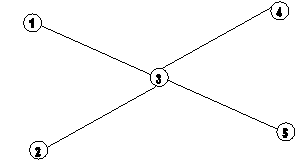
оставаться связным. Например, пусть метро выглядит так, как показано
на рисунке. Тогда станции можно закрывать, например, в порядке 1, 2,
4, 3, 5. А порядок 3, 1, 2, 4, 5 - не подходит, так как после
закрытия 3-й станции метро распадется на четыре не связных между
собой части.
Ввод. Первая
строка входного файла будет содержать числа N и M. В следующих M
строках находится информация о линиях. Каждая из этих строк содержит
через пробел числа Ai и Bi (Ai Bi) - две станции, которые соединяет
i-я линия.
Вывод. Выходной файл должен состоять из N строк. Каждая
строка должна содержать одно число - номер станции. Вывести станции
нужно в порядке их закрытия.
Пример
input.txt
5 4
3 1
3 2
3 4
3 5
output.txt
1
2
4
3
5
 Решение:
Решение:
Сначала я вспомнил самарское метро и решил, что эта задача очень
похожа на задачу - Михаил Густокашин против бюрократии. Но
потом я вспомнил московское метро (кольцевую линию) и понял, что
этот метод не пройдет. По крайней мере не пройдет с теми входными
данными, которые нам даны.
Перед тем, как воспользоваться алгоритмом из той задачи надо
преобразовать данный нам граф в его остовное дерево. Остовным
деревом графа называется правильное дерево, включающее все вершины
графа. Его несложно сгенирировать воспользовавшись поиском в графе в
глубину.
Заведем две таблицы смежности - одну для данного графа, другую для
остовного дерева. Запустим рекурсивную процедуру посика в глубину,
она будет выглядеть примерно так:
1) помечаем, что данная вершина входит в дерево.
2) для всех вершин, смежных с данной, но еще не включенных в дерево,
запускаем рекрсивную процедуру поиска в глубину.
3) для всех вершин, для которых мы запускали рекурсивную процедуру
поиска в глубину, в таблице смежности для остовного дерева отмечаем
наличие ребра между данной вершиной и вершиной, для которой мы
запускали рекрсивную процедуру.
Вот вроде бы и вся процедура, работает она за O(n^2). Теперь у нас
есть дерево, будем отрезать его листья и трансормировать ветки в
листья, при необходимости.
Пройдем по всем вершинам дерева и найдем те из них, которые имеют
только одно ребро. Удалим эту вершину, а также отметим отсутствие
данного ребра в таблице смежности. Выведем номер удаленной вершины.
Будем повторять этот процесс, да тех пор, пока не останется
единственная вершина - выведем ее номер. Сложность этого алгоритма O(n^3),
при максимальном значении n - 10^9 - достаточно большая, но если
применить некоторые оптимизации, то программа будет отлично
укладываться во временные рамки.
Далее
ð
