Задача 61: Бизнес-классики (XIII Всероссийская олимпиада по
информатике)
Поле для игры в бизнес-классики
представляет собой прямоугольник, состоящий из 3 * N клеток. В
некоторых клетках лежит по одному рублю, в остальных - ничего нет.
Играющий выбирает для начала игры одну из трех левых клеток и
прыгает в нее. За один ход играющий перепрыгивает в одну из клеток,
имеющих общую сторону с той, в которой он находится. При этом
запрещено прыгать в те клетки, в которых он уже побывал. При
очередном прыжке все деньги, собранные к этому моменту, удваиваются,
а затем, если в новой клетке лежит рубль, то он прибавляется к
имеющейся сумме денег. Считается, что в начале игры денег у
играющего нет. Закончить прыжки надо в одной из трех правых клеток
поля и при этом заработать как можно больше денег.
Требуется написать программу, которая по известному значению N и
расположению рублей в клетках находит такую последовательность
прыжков, при которой играющий заработает наибольшее количество
денег. Если таких последовательностей несколько, то следует выбрать
любую последовательность, количество прыжков в которой минимально.
Входные данные
В первой строке входного файла с именем CLASS.IN записано
натуральное число N (1 < N < 80). В каждой из последующих трех строк
находится N чисел (0 или 1), описывающих расположение рублей в
клетках первой, второй и третьей строки игрового поля
соответственно. Единица обозначает наличие рубля в клетке, ноль -
его отсутствие. Числа в каждой из этих трех строк входного файла
расположены через пробел.
Выходные данные
Выходной файл с именем CLASS.OUT должен содержать 2 строки. В
первой строке должен находиться номер строки игрового поля (1, 2 или
3), с которой играющему следует начать игру. Вторая строка файла
должна описывать последовательность прыжков. Каждый прыжок в этой
последовательности нужно обозначить одним из следующих символов:
U - если в результате прыжка номер строки, на которой находится
играющий, уменьшился на 1;
D - если номер строки увеличился на 1;
L - если номер столбца уменьшился на 1;
R - если номер столбца увеличился на 1.
Символы во второй строке выходного файла должны быть выведены без
пробелов.
Пример входного файла
4
1 1 1 0
1 1 1 0
1 1 1 1
Пример выходного файла для приведенного примера входного
файла
1
DDRUURDDRUU
 Решение: предоставлено
Е.В. Андреевой
Решение: предоставлено
Е.В. Андреевой
Если, согласно информации о наличии или отсутствии рублей в клетках,
искомую последовательность прыжков записать в виде набора нулей и
единиц, то станет ясно, что размер выигрыша равен значению
полученного двоичного числа. Так, в приведенном примере игрок
заработает 1111111111002 = 409210 . Отсюда следует, что в
большинстве случаев игроку выгодно побывать во всех клетках поля, в
этом случае число разрядов двоичного числа будет максимальным, а
количество прыжков равно 3N. Меньшее количество прыжков имеет смысл
делать лишь если рублей на поле нет совсем (тогда выигрыш будет
равен 0 для любой последовательности прыжков, а последовательность
прыжков минимальной длины будет состоять из N клеток любой строки)
или если первый столбец имеет вид 010 (тогда значение выигрыша
выражается двоичным числом длины 3N-1 и игрок может впрыгивать в
среднюю клетку, не уменьшая выигрыша). Во всех остальных случаях
впрыгивать имеет смысл только в начальную клетку первой или третьей
строки, иначе невозможно побывать во всех клетках поля, не нарушая
правила игры.
Осталось определить способ обхода всех клеток поля, который будет
соответствовать максимально возможному двоичному числу. В связи с
тем что поле имеет всего три строки, каждые из k рядом стоящих
столбцов могут быть пройдены одним из двух способов - вертикальной
или горизонтальной "змейкой" (решение в примере соответствует
прохождению всех столбцов поля вертикальной "змейкой"). А все поле
целиком можно обойти, комбинируя эти два способа: например, первые
k1 столбцов - вертикальной "змейкой", следующие k2 - горизонтальной,
следующие k3 - опять горизонтальной - и т.д. - см. рис. 1.
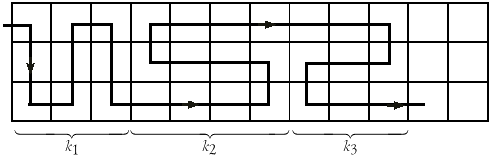
Рис.1.
Пусть мы уже знаем
оптимальный способ обхода первого столбца, первых двух столбцов, :,
первых k - 1 столбцов. Тогда несложно определить оптимальный способ
обхода первых k столбцов, сравнивая результаты следующих комбинаций
обхода - обход горизонтальной "змейкой" всех первых k столбцов
сверху вниз или снизу вверх или оптимальный обход первого столбца +
горизонтальная "змейка" по следующим k - 1 столбцам или оптимальный
обход первых двух столбцов + горизонтальная "змейка" по следующим k
- 2 столбцам и т.д. Последний из рассматриваемых вариантов
представляет собой оптимальный обход первых k - 1 столбцов и
вертикальное прохождение k-го столбца. Наилучшая из рассмотренных
комбинаций запоминается как оптимальный обход k первых столбцов и
используется в дальнейшем. Такой способ решения относится к
динамическому программированию.
Далее
ð
