Задача 51: Оппозиция (XIII Всероссийская
олимпиада по информатике)
В некоторой стране полиция выявила разветвленную сеть оппозиционной
партии.
Партия сильно законспирирована и состоит из рядовых членов и
руководителей различных уровней. Во главе партии стоит один главный
руководитель - лидер партии. До начала арестов приказ лидера может
быть доведен до любого члена партии. Все члены партии пронумерованы
от 1 до N.
Каждый член партии знает только своего вышестоящего руководителя
(ровно одного) и своих непосредственных подчиненных (руководитель не
знает подчиненных своего подчиненного и наоборот).
Естественно, что с началом арестов членов партии она распадется на
мелкие, не связанные друг с другом группы. Например, с арестом члена
партии № 2 (см. рис. 2) партия разваливается на 4 группы.
Полицмейстер уверяет, что группа, состоящая из менее чем К членов
партии, идеологически вырождается и не представляет угрозы для
государства.
Стремясь не уронить престиж страны в глазах мирового общественного
мнения, полицмейстер поставил задачу произвести минимальное
количество арестов членов партии так, чтобы от нее остались только
идеологически вырождающиеся маленькие группы.
Требуется
Написать программу, которая бы по входным данным, описывающим
структуру подпольной партии, выводила количество арестов и номера
членов партии, которых нужно арестовать.
Входные данные
Входной файл с именем ORG.IN содержит три строки. В первой записано
число K (1 < K < 10 000), во второй строке - число N (1 ? N ? 10
000), определяющее количество членов партии. Третья строка содержит
набор из N-1 числа. В этой строке для каждого члена партии, кроме
лидера, задается номер его непосредственного руководителя. Номер
руководителя всегда меньше, чем номер подчиненного. При этом первое
число задает номер руководителя второго члена партии, второе -
третьего и так далее. Числа в строке разделяются одним пробелом.
Выходные данные
Выходной файл с именем ORG.OUT состоит из двух строк. В первую
строку необходимо поместить количество арестов, а во вторую - номера
членов партии, подлежащих аресту. Эти номера разделяются одним
пробелом. При наличии нескольких решений выведите одно из них.
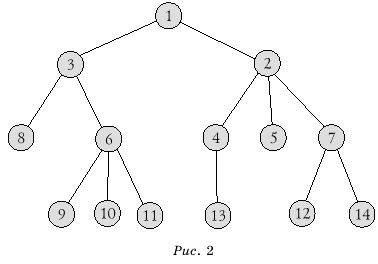
Пример входного
файла для структуры партии, представленной на рис. 2
3
14
1 1 2 2 3 2 3 6 6 6 7 4 7
Пример выходного файла для приведенного входного файла
4
6 2 7 8
 Решение:
предоставлено Е.В. Андреевой
Решение:
предоставлено Е.В. Андреевой
Описанная в условии задачи структура партии представляет собой
дерево. Пусть для некоторого его поддерева справедливо следующее:
каждая ветвь данного поддерева в отдельности содержит менее K
элементов, а все поддерево в целом - K или более элементов (число
элементов в поддереве равно сумме элементов в его ветвях плюс один
элемент, соответствующий корневой вершине поддерева). Тогда
очевидно, что удаление корневой вершины данного поддерева (то есть
арест соответствующего члена партии) решает поставленную задачу в
рамках рассмотренного поддерева оптимальным образом.
Действительно, удаление вершин, не принадлежащих данному поддереву,
не может уменьшить избыточное число элементов в нашем поддереве, а
удаление иной вершины поддерева, кроме корневой, возможно, и
приведет к решению задачи для рассмотренного поддерева, но тогда
непосредственный "начальник" неудаленной корневой вершины
"идеологически обезвреженного" поддерева будет иметь по крайней мере
на одного "подчиненного" больше, что может увеличить общее число
удалений вершин (арестов).
В результате получаем следующий алгоритм решения задачи. Начиная с
"листовых" вершин (соответствующих рядовым членам партии, не имеющим
подчиненных), подсчитываем для каждой вершины дерева количество
элементов в связанном с ней поддереве. Если количество элементов в
поддереве оказалось больше или равно K, то его корневая вершина
удаляется, данное поддерево исключается из рассмотрения и задача
решается для оставшихся элементов дерева. Последним из рассмотренных
элементов должна оказаться вершина № 1, обозначающая лидера партии.
Так, в приведенном примере данный алгоритм предложит удалить вершины
дерева с номерами 7, 6, 2 и 1. Алгоритм является линейным
относительно количества членов партии, а его реализация зависит от
выбора структуры данных для хранения исходного дерева.
Далее
ð
