Линейные алгоритмы. Задачи повышенной сложности

Задачи повышенной сложности

ЦЕЛОЧИСЛЕННАЯ АРИФМЕТИКА

1. Часовая стрелка образует угол у с лучом, проходящим через центр и через точку, соответствующую 12 часам на циферблате, 0 < у < 2я. Определить значение угла для минутной стрелки, а также количество часов и полных минут.

2. Даны целые числа h, т (0 < h < 12,0 < т < 59), указывающие момент времени: «й часов, т минут». Определить наименьшее время (число полных минут), которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате

а) совпадут;

б) расположатся перпендикулярно друг другу.

3. Даны целое число k (I < k < 180) и последовательность цифр 10111213...9899, в которой выписаны подряд все двузначные числа. Определить:

а) номер пары цифр, в которую входит k-я цифра;

б) двузначное число, образованное парой цифр, в которую
входит k-я цифра;

в) k-ю цифру, если известно, что:

• к — четное число;

• k — нечетное число.

4. Даны целое число k (I < k < 150) и последовательность цифр 101102103...149150, в которой выписаны подряд все трехзначные числа от 101 до 150. Определить k-ю цифру, если известно, что:

• k — число, кратное трем;

• k — одно из чисел 1, 4, 7 ...;

• k — одно из чисел 2, 5, 8 ...

ВЕЛИЧИНЫ ЛОГИЧЕСКОГО ТИПА

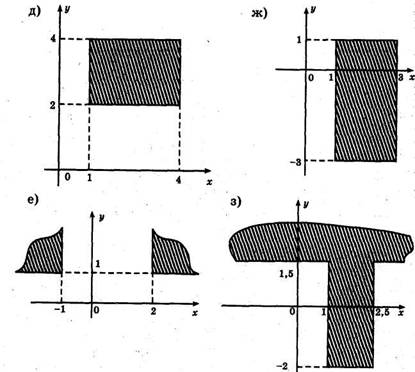
1. Записать условие, которое является истинным, когда точка с координатами х, у попадает в заштрихованные участки плоскости.

2. Поле шахматной доски определяется парой натуральных Чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа — а, Ъ, с, d, каждое из которых не превосходит восьми.

а) На поле (а, Ь) расположена ладья. Записать условие, при котором она угрожает полю (с, d).

б) На поле (а, Ь) расположен слон. Записать условие, при котором он угрожает полю (с, d).

в) На поле (а, Ь) расположен король. Записать условие, при котором он может одним ходом попасть на поле (с, d).

г) На поле (а, Ь) расположен ферзь. Записать условие, при котором он угрожает полю (с, d).

д) На поле (а, Ь) расположена белая пешка. Записать условие, при котором она может одним ходом попасть на поле (с, d):

• при обычном ходе;

• когда она «бьет» фигуру или пешку соперника.
Белые пешки перемещаются на доске снизу вверх.

е) На поле (а, Ь) расположена черная пешка. Записать условие, при котором она может одним ходом попасть на поле (с, d):

• при обычном ходе;

• когда она «бьет» фигуру или пешку соперника.
Черные пешки перемещаются на доске сверху вниз.

ж) На поле (а, Ь) расположен конь. Записать условие, при
котором он угрожает полю (с, d).

3. Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа — а, Ъ, с, d, e, f, каждое из которых не превосходит восьми. Записать условие, при котором белая фигура, расположенная на поле (а, Ь), может одним ходом пойти на поле (е, /), не попав при этом под удар черной фигуры, находящейся на поле {с, d). Рассмотреть следующие варианты сочетаний белой и черной фигур:

а) ладья и ладья; л) конь и ферзь;

б) ладья и ферзь; м) конь и слон;

в) ладья и конь; н) слон и слон;

г) ладья и слон; о) слон и ферзь;

д) ферзь и ферзь; п) слон и конь;

е) ферзь и ладья; р) слон и ладья;

ж) ферзь и конь; с) король и слон;

з)   ферзь и слон;                       т) король и ферзь;
и) конь и конь;                           у) король и конь;
к) конь и ладья;                         ф) король и ладья.